模板及讲解
分治
分治关键为
1、分 (分区间)
2、解 (解小范围的答案)
3、并 (合并分的两个区间,处理跨区间的答案)
归并排序、逆序对
棋盘覆盖
最大连续子序列和
例题:Hdu 1003
求最大连续子序列和。
我们可以将区间一分为二,然后对两个区间求出最大连续子序列和,然后合并时考虑在两边的答案,在中间的答案。对于在中间的答案,我们需要求出左边区间右边开始最大连续子序列和大小,右边区间左边开始的最大连续子序列和大小。然后合并即可。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<utility>
#include<cmath>
#define ms(i, j) memset(i, j, sizeof i)
#define LL long long
#define db double
#define fir first
#define sec second
#define mp make_pair
using namespace std;
int T, kse = 0;
namespace flyinthesky {
const int MAXN = 100000 + 5;
int n, a[MAXN];
int dc(int l, int r, int &x, int &y) {
if (l == r) {
x = y = l;
return a[l];
}
int mid = (l + r) >> 1;
int ans1, l1, r1; ans1 = dc(l, mid, l1, r1);
int ans2, l2, r2; ans2 = dc(mid + 1, r, l2, r2);
int maxrs = -1000000000, rs = 0, r3 = mid + 1;
for (int i = mid + 1; i <= r; ++i) {
rs += a[i];
if (rs > maxrs) maxrs = rs, r3 = i;
}
int maxls = -1000000000, ls = 0, l3 = mid;
for (int i = mid; i >= l; --i) {
ls += a[i];
if (ls > maxls) maxls = ls, l3 = i; else if (ls == maxls) l3 = i;
}
if (ans1 < ans2) {
ans1 = ans2;
l1 = l2, r1 = r2;
} else if (ans1 == ans2) {
if (l1 > l2) l1 = l2, r1 = r2;
}
if (ans1 < maxls + maxrs) {
ans1 = maxls + maxrs;
l1 = l3, r1 = r3;
} else if (ans1 == maxls + maxrs) {
if (l1 > l3) l1 = l3, r1 = r3;
}
x = l1, y = r1;
return ans1;
}
void clean() {
}
int solve() {
clean();
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
int g1, g2;
int ans = dc(1, n, g1, g2);
printf("Case %d:\n%d %d %d\n", ++kse, ans, g1, g2);
if (T) printf("\n");
return 0;
}
}
int main() {
scanf("%d", &T);
while (T--) flyinthesky::solve();
return 0;
}
最近点对问题
例题:Luogu 1429
给定平面上$n$个点,找出其中的一对点的距离,使得在这$n$个点的所有点对中,该距离为所有点对中最小的
(以下内容来自http://jvruo.com/archives/84/)
一维
$n$个点退化为$x$轴上的$n$个实数$x_1,x_2,…,x_n$。最近点对即为这$n$个实数中相差最小的两个实数。显然可以先将点排好序,然后用$O(n)$线性扫描。但为了便于推广到二维的情形,尝试用分治法解决这个问题。
首先肯定要先对点进行排序,接着假设我们用$m$点将$S$分为$S_1$和$S_2$两个集合,这样对于所有的$p(S_1$中的点)和$q(S_2$中的点),有$p < q$。
然后把$S_1$和$S_2$分别当作完整的序列$S$,分治地在$S_1$和$S_2$上找出其最近点对,并设$ d $为两个集合的最近点对长度
由此,$S$中最近点对可能是在$S_1$中的,可能是在$S_2$中的,也可能是跨越两个集合的。
如果此时最近点对是跨越两个集合的,则集合两点与$m$的距离都不超过$d$,且一定分别出现在区间$(m-d,d]$和$(d,m+d]$。并且只有一对这样的点对。时间复杂度为$O(nlogn)$。
二维
我们可以对刚刚的做法进行推广,首先先对$x$坐标进行排序,取出中点,然后对于左右两边的区域$S_1,S_2$,重复上述过程,递归地求出左右两边分别的最近点对的距离$d_1,d_2$,并且$d=min(d_1,d_2)$。
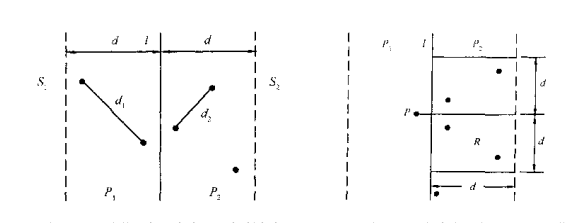
接着我们来考虑跨越集合的情况,由左图可见(注: $l:x=m$),由于可能的点只会落在$(m-d,m+d)$的宽为$2d$的带状区间内,但最多可能有$n$个点,合并时间最坏情况下为$O(n^2)$。然而,$P_1$和$P_2$中的点具有一种稀疏的性质——对于$P_1$中的任意一点,$P_2$中的点必定落在一个$d \times 2d$(如右图,不然$P_1,P_2$之间的距离$d_3$一定大于$d$,可反证 ,相当于将$y$坐标投影到直线$l$上)的矩形中,且最多只需检查六个点(鸽巢原理,后面会证明)。那么我们可以先将带状区间的点按$y$坐标排序,然后扫描,这样合并的时间复杂度$O(nlogn)$。总的时间复杂度为$O(nlognlogn)$。
最多六个节点的证明:
因为$d=min(d_1,d_2)$,所以这个$d \times 2d$的矩形中,任意两点的之间的距离都要大于等于$d$。那么我们想在这个$d \times 2d$的矩形中放尽量多的点,并且彼此之间距离都要大于等于$d$。
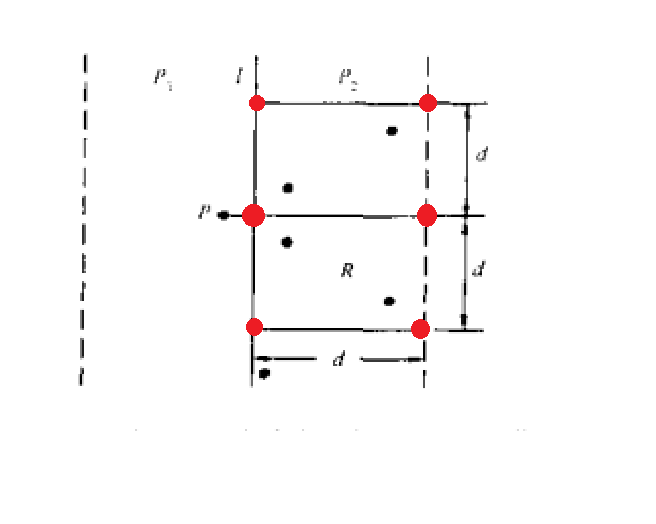
按照上图的红点位置放,是最优的策略。此时最多只能放下六个点。所以原结论是正确的。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<utility>
#include<cmath>
#define ms(i, j) memset(i, j, sizeof i)
#define LL long long
#define db double
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace flyinthesky {
const int MAXN = 200000 + 5;
struct node {
db x, y;
}p[MAXN], f[MAXN];
int n;
bool cmp1(node a, node b) {return a.x < b.x;}
bool cmp2(node a, node b) {return a.y < b.y;}
db dist(node a, node b) {
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
db dc(int l, int r) {
if (l == r) return 2e9;
if (l == r - 1) return dist(p[l], p[r]);
int mid = (l + r) >> 1, tot = 0;
db d1 = dc(l, mid);
db d2 = dc(mid + 1, r);
db d = min(d1, d2);
for (int i = l; i <= r; ++i) if (fabs(p[i].x - p[mid].x) <= d) f[++tot] = p[i];
sort(f + 1, f + 1 + tot, cmp2);
for (int i = 1; i <= tot; ++i) {
for (int j = i + 1; j <= tot; ++j) {
if (f[j].y - f[i].y <= d) {
db tmp = dist(f[i], f[j]);
if (tmp < d) d = tmp;
} else break;
}
}
return d;
}
void clean() {
}
int solve() {
clean();
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
sort(p + 1, p + 1 + n, cmp1);
printf("%.4f\n", dc(1, n));
return 0;
}
}
int main() {
flyinthesky::solve();
return 0;
}
