Codeforces 1013D
题意：一个矩形的其中三个顶点有东西的话第四个顶点也会有东西, 然后问你铺满网格最少需要买多少东西。

维护行列方法：并查集、图论、2-SAT、二分图
这里用并查集。我们根据三个点坐标，发现如果连上$(r1, c1), (r1, c2), (r2, c1)$无向边，则$(r2, c2)$连通，相当于这个点存在了。所以我们用并查集连边，判断连通块个数$siz$，买$siz-1$个点使得整个图连通即可。

Codeforces 940E
题意：给你一个长为$n$的序列和一个数字$c$，你要将这个序列切成若干段，对于每一段，这段中最小的$\frac nc$个数字（向下取整）都会被自动删除，问怎么切割使最后剩下的数字和最小

可以证明一段长度不会超过$c$。假设有一段长度超过$c$，因为超过$c$的部分不能给这个段提供更大的删除值，而如果长度为$xc$($x$为任意正整数)，那么这个段可以分成$x$段$c$长度的段，并且答案可能更优。那么每一段长度等于$c$的段就只用删除一个数。
所以我们设$dp(i)$为前$i$个数删除数值的最大值，那么$dp(i)=dp(i-c)+min(a_j|i - c + 1 \leq j \leq i)$，删区间$[i-c+1, i]$最小的数。也有可能$i$点不取最优(在此处后面断开)，则$dp(i)=dp(i-1)$。

知识点：本题 DP 状态使用了补集转化思想，并且利用$dp(i)=dp(i-1)$来处理段长不为$c$的情况。

模板及讲解

分治

分治关键为
1、分 (分区间)
2、解 (解小范围的答案)
3、并 (合并分的两个区间，处理跨区间的答案)

归并排序、逆序对

棋盘覆盖

最大连续子序列和

例题：Hdu 1003

求最大连续子序列和。

我们可以将区间一分为二，然后对两个区间求出最大连续子序列和，然后合并时考虑在两边的答案，在中间的答案。对于在中间的答案，我们需要求出左边区间右边开始最大连续子序列和大小，右边区间左边开始的最大连续子序列和大小。然后合并即可。

#include<cstdio> 
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<utility>
#include<cmath>
#define ms(i, j) memset(i, j, sizeof i)
#define LL long long
#define db double
#define fir first
#define sec second
#define mp make_pair
using namespace std;

int T, kse = 0;

namespace flyinthesky {

    const int MAXN = 100000 + 5;

    int n, a[MAXN];

    int dc(int l, int r, int &x, int &y) {

        if (l == r) {
            x = y = l;
            return a[l];
        }

        int mid = (l + r) >> 1;
        int ans1, l1, r1; ans1 = dc(l, mid, l1, r1);
        int ans2, l2, r2; ans2 = dc(mid + 1, r, l2, r2);
        int maxrs = -1000000000, rs = 0, r3 = mid + 1;
        for (int i = mid + 1; i <= r; ++i) {
            rs += a[i];
            if (rs > maxrs) maxrs = rs, r3 = i;
        }
        int maxls = -1000000000, ls = 0, l3 = mid;
        for (int i = mid; i >= l; --i) {
            ls += a[i];
            if (ls > maxls) maxls = ls, l3 = i; else if (ls == maxls) l3 = i;
        }

        if (ans1 < ans2) {
            ans1 = ans2;
            l1 = l2, r1 = r2;
        } else if (ans1 == ans2) {
            if (l1 > l2) l1 = l2, r1 = r2;
        }
        if (ans1 < maxls + maxrs) {
            ans1 = maxls + maxrs;
            l1 = l3, r1 = r3;
        } else if (ans1 == maxls + maxrs) {
            if (l1 > l3) l1 = l3, r1 = r3;
        }
        x = l1, y = r1;
        return ans1;
    }

    void clean() {
    }
    int solve() {
        clean();
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
        int g1, g2;
        int ans = dc(1, n, g1, g2);
        printf("Case %d:\n%d %d %d\n", ++kse, ans, g1, g2);
        if (T) printf("\n");
        return 0; 
    }
}
int main() {
    scanf("%d", &T);
    while (T--) flyinthesky::solve();
    return 0;
}

最近点对问题

例题：Luogu 1429

给定平面上$n$个点，找出其中的一对点的距离，使得在这$n$个点的所有点对中，该距离为所有点对中最小的

(以下内容来自http://jvruo.com/archives/84/)

一维

$n$个点退化为$x$轴上的$n$个实数$x_1，x_2，…，x_n$。最近点对即为这$n$个实数中相差最小的两个实数。显然可以先将点排好序，然后用$O(n)$线性扫描。但为了便于推广到二维的情形，尝试用分治法解决这个问题。

首先肯定要先对点进行排序，接着假设我们用$m$点将$S$分为$S_1$和$S_2$两个集合，这样对于所有的$p(S_1$中的点)和$q(S_2$中的点)，有$p < q$。

然后把$S_1$和$S_2$分别当作完整的序列$S$，分治地在$S_1$和$S_2$上找出其最近点对，并设$ d $为两个集合的最近点对长度

由此，$S$中最近点对可能是在$S_1$中的，可能是在$S_2$中的，也可能是跨越两个集合的。

如果此时最近点对是跨越两个集合的，则集合两点与$m$的距离都不超过$d$，且一定分别出现在区间$(m-d,d]$和$(d,m+d]$。并且只有一对这样的点对。时间复杂度为$O(nlogn)$。

二维

我们可以对刚刚的做法进行推广，首先先对$x$坐标进行排序，取出中点，然后对于左右两边的区域$S_1，S_2$，重复上述过程，递归地求出左右两边分别的最近点对的距离$d_1，d_2$，并且$d=min(d_1,d_2)$。

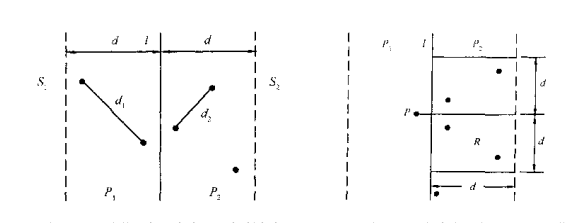
接着我们来考虑跨越集合的情况，由左图可见(注: $l:x=m$)，由于可能的点只会落在$(m-d，m+d)$的宽为$2d$的带状区间内，但最多可能有$n$个点，合并时间最坏情况下为$O(n^2)$。然而，$P_1$和$P_2$中的点具有一种稀疏的性质——对于$P_1$中的任意一点，$P_2$中的点必定落在一个$d \times 2d$(如右图，不然$P_1，P_2$之间的距离$d_3$一定大于$d$，可反证 ，相当于将$y$坐标投影到直线$l$上)的矩形中，且最多只需检查六个点（鸽巢原理，后面会证明）。那么我们可以先将带状区间的点按$y$坐标排序，然后扫描，这样合并的时间复杂度$O(nlogn)$。总的时间复杂度为$O(nlognlogn)$。

最多六个节点的证明：

因为$d=min(d_1,d_2)$，所以这个$d \times 2d$的矩形中，任意两点的之间的距离都要大于等于$d$。那么我们想在这个$d \times 2d$的矩形中放尽量多的点，并且彼此之间距离都要大于等于$d$。

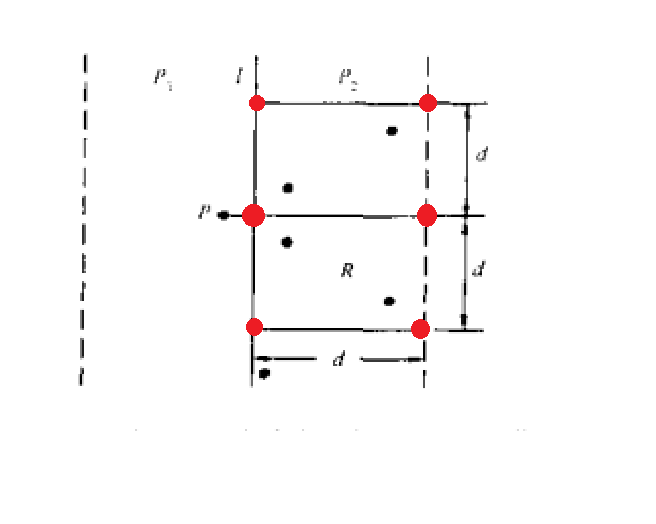
按照上图的红点位置放，是最优的策略。此时最多只能放下六个点。所以原结论是正确的。

#include<cstdio> 
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<utility>
#include<cmath>
#define ms(i, j) memset(i, j, sizeof i)
#define LL long long
#define db double
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace flyinthesky {
    const int MAXN = 200000 + 5;

    struct node {
        db x, y;
    }p[MAXN], f[MAXN];

    int n;

    bool cmp1(node a, node b) {return a.x < b.x;}
    bool cmp2(node a, node b) {return a.y < b.y;}

    db dist(node a, node b) {
        return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
    }
    db dc(int l, int r) {
        if (l == r) return 2e9; 
        if (l == r - 1) return dist(p[l], p[r]);
        int mid = (l + r) >> 1, tot = 0;
        db d1 = dc(l, mid);
        db d2 = dc(mid + 1, r);
        db d = min(d1, d2);
        for (int i = l; i <= r; ++i) if (fabs(p[i].x - p[mid].x) <= d) f[++tot] = p[i];
        sort(f + 1, f + 1 + tot, cmp2);
        for (int i = 1; i <= tot; ++i) {
            for (int j = i + 1; j <= tot; ++j) {
                if (f[j].y - f[i].y <= d) {
                    db tmp = dist(f[i], f[j]);
                    if (tmp < d) d = tmp; 
                } else break;
            }
        } 
        return d;
    }
    void clean() {
    }
    int solve() {
        clean();
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
        sort(p + 1, p + 1 + n, cmp1);
        printf("%.4f\n", dc(1, n));
        return 0; 
    }
}
int main() {
    flyinthesky::solve();
    return 0;
}

常见题型

模板及讲解

三分和二分区别

二分法用于单调函数上逼近某值，而三分法用于单峰函数 (凸函数/凹函数)上逼近极值点。

基本思路

对于区间$[l,r]$，我们求出$[l,r]$中点$mid$，再求出$[mid,r]$的中点$mmid$.

如果$f(mid) > f(mmid)$，那么$mmid$在极值点右边。
如果$f(mid) < f(mmid)$，那么$mmid$在极值点左边。

以上直接用反证法可以证明，根据单调性的定义。

然后就可以用这个方法来更新了，最后$l,r$大的那个点是极值点。

Codeforces 982D
题意：有一只鲨鱼每天游$a_i$公里，如果它一天游的距离大于等于$k$，我们就认为它游到了一个新的地方；否则认为它这一天停留在原来的地方。这只鲨鱼到过的地方不会重复。现在给出它$n$天游的距离（每天都不相等），我们要求出一个$k$，满足：
1.鲨鱼停留在每个地方的天数相等。（一天游的距离大于等于$k$时不算停留）。
2.停留过的地方尽可能多。
3.有多个解时$k$取最小值。

很容易想到答案就是某个$a_i+1$，并且没有单调性，不能二分。
另一个角度想，因为每天都不相等，所以我们按照从小到大按顺序将每个点加入，形成几个区间。就变成了区间合并问题。如果加的数左右都没有区间，就新建一个区间。左边或者右边有，扩展区间。都有的话就直接合并区间。然后为了每个区间大小相等，就用当前最长的区间大小乘以当前区间个数如果等于已经插入的点，那么一定每个区间大小相等，更新答案即可。

BZOJ 1497
题意：有$n$个结点，$m$条无向边可供建设。
建立一个结点$u$有一定的花费$p_u$。建立一条无向边有一定的非负收益$w_e$。
建立一条无向边$(u, v)$的必要条件是要先建立点$u$，点$v$。
求最大获利。

将点、边作为事件，边$(u, v)$依赖点$u,v$，即转化为一个最大权闭合子图问题。
将边拆成点，按最大权闭合子图问题做即可。

SPOJ-COT2
题意：给一棵树，每个点有一个权值。多次询问路径$(u, v)$上有多少个权值不同的点。
树上莫队的资料
考虑树上莫队。难点在于怎么将树搬到序列中。将树的括号序求出来，树的括号序就是维护一个序列，这个序列是dfs这棵树时，每个节点在dfs到的时候将本身加入序列，然后离开该节点(返回父节点)也将本身加入序列的一个序列(具体可以看资料，有图解)。
我们设$st,ed$分别为某个点最开始在序列出现位置和最后出现在序列的位置。对于一条路径$(u,v)$(这里$st_u \leq st_v$)：
如果$LCA=u$，那么路径就是$st_u$到$st_v$之间一段中出现次数为奇数次的点。
否则，路径就是$ed_u$到$st_v$之间一段中出现次数为奇数次的点。注意这一段并不包含LCA，要手动加上。
然后就是注意莫队转移的时候的方法，用奇偶性判断这个节点出现几次，只考虑奇偶性。奇数就可以让记录权值出现次数的数组加一，反之减一。

BZOJ 4241
题意：有一个长度为$n$的序列，有$m$个询问，每次询问「$[l, r]$内每个数值乘以该数值出现次数」的最大值。

分块做法(在线)：
预处理$s(i,j)$为$i$块到$j$块的答案最优的那个数值是什么，然后像区间众数一样做，询问的时候直接不完整块查询出现次数更新答案，整块就用之前预处理的数值来查询

莫队做法(离线)：
由于删除更新答案不方便，那么这里可以用回滚莫队。按照原莫队方法排序，那么左端点在一块的询问就到了一起，并且右端点单调递增，右端点只有增加，考虑左端点。要使得左端点只能增加，我们把所有在一个块的左端点的询问一起处理，都将莫队中的左端点移到块最右边，每次查询的时候就从最右边开始向左延伸，记录答案，然后再回退到块最右边，这样就避免了删除。一个块处理完后，因为右端点会有删除的情况，所以直接抛弃之前的所有答案，重新从新询问开始记录答案。对于左右端点在同块的询问，直接暴力即可。
时间复杂度分析：
1、对于左右端点在同块的询问，其时间复杂度最坏为$O(m\sqrt n)$
2、在同块中处理时，右端点单调递增，最多增加$n$次，复杂度$O(n\sqrt n)$。左端点回滚，由于在块中，最多滚动$\sqrt n$次，复杂度$O(m\sqrt n)$。
3、对于左端点不同块之间的转换，清除记录数组时间复杂度$O(n\sqrt n)$
由于$m,n$同级，所有算法复杂度为$O(n\sqrt n)$
比分块快多了

BZOJ 2821
题意：求区间内出现次数为正偶数的数字的个数。

老套路，这种能方便将点加入答案的题目，维护$s(i,j)$为$i$块到$j$块出现次数为正偶数的数的个数(块到块节约空间)，然后整块就处理完了，不完整块就每个数查询一下这个数出现在整块的次数和$[l,r]$的次数，用奇偶性判断是否要增加/减少答案。

BZOJ 3744
题意：强制在线不修改求区间逆序对。

比较容易想到一个做法：用树状数组维护$[1, i]$逆序对数目，然后每个询问$[l,r]$就用$[1,r]$的答案再去除$[1,l-1]$的答案，去除方法是枚举每个$[1,l-1]$的数，在之后$[l, r]$区间找比他小的数的个数，答案减去这个个数即可，可以用树状数组/主席树维护(前缀和)，时间复杂度很高，高达$O(mnlog_n)$

我们可以优化，可以用分块优化暴力枚举。预处理出$s(i,j)$表示第$i$个块最开始的位置到点$j$之间逆序对的个数，用树状数组维护即可，时间复杂度$O(n\sqrt n)$
对于询问，如果$l,r$在同一块，直接树状数组暴力统计，因为在块中。
不在一块的话，找$l$在的块的后面一块，运用$s(i,j)$直接将后面所有的逆序对都处理完了，然后考虑前面不整块，与前面说的容易想到的方法一样，直接做就行，因为在块中所有枚举量被大大减小。